Exponential Smoothing
Contents
指数平滑(exponential smoothing)和ARIMA一样也是一个使用很广泛的时间序列预测模型,基于指数平滑模型的预测对于过去观测量的一个加权平均,不过这里的加权平均和ARIMA不一样,并非线性加权,这里的权重会随着以往观测量变得久远而不断衰减。换句话说,就是距离当前预测越近的观测量,它的权重越高。
1. Simple exponential smoothing
最简单的模型就是simple exponential smoothing(SME),这个方法适用于那些没有clear trend or seasonal pattern的序列。如下图是几年间某个地区油的产量,这个序列并没有表现出很清晰的趋势或者周期性(当然最近几年有过一个上升阶段,这可能代表着某种趋势,这个以后再讨论有没有更高级的方法去建模)。我们现在只考虑用简单的naive和average方式做预测。
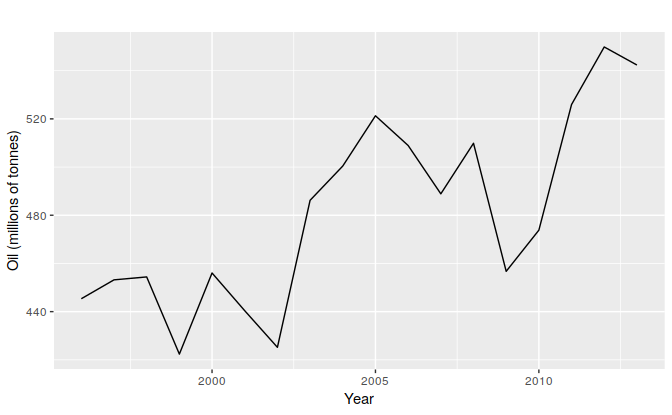
使用naive方法,有如下预测,这相当于忽略了之前所有信息,之用前一个,也就是把weight全都给了前一个时间点的值。
$$
\hat{y}_{T+h|T}=y_T
$$
使用average方法,则有如下预测,就相当于给之前预测都是平均的weight。
$$
y_{T+h|T}=\frac{1}{T} \sum_{t=1}^T y_t
$$
上述两个其实是两个极端现象,更合理的情况是我们想让离预测点近的值权重更大,而离的远的值权重小一些。这其实也是SEM背后隐藏的思想,所以可以用如下方式对SEM建模。
$$
\hat{y}_{T+1|T}=\alpha y_T+\alpha(1-\alpha)y_{T-1}+\alpha(1-\alpha)^2y_{T-2}+\ldots
$$
参数$0<\alpha<1$就是smoothing parameter,所以权重衰减是由参数$\alpha$控制的。下面是参数$\alpha$取不同值的权重衰减情况。可以看出只要参数在0到1之间,权重就会随时间的变化呈现指数形式不断衰减,所以这也是exponential smoothing的由来。
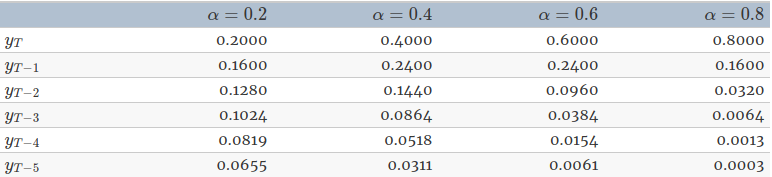
下面我们给出两种和上述SEM模型等价的表达式:
1.1. Weighted Average Form
$$
\hat{y}_{T+1|t} = \alpha y_T + (1-\alpha)\hat{y}_{T|T-1}
$$
这其实是一种迭代的方式给出的公式,只要从序列的开始进行建模,逐层带进去最后的计算结果和标准的SEM形式一致。
1.2. Component Form
另外一种方式叫做成分表达式,对于SEM来说,我们只有单一的成分也就是level,$l_t$,之后的其他方法可能会涉及其他的成分,比如趋势成分trend component $b_t$和周期成分seasonal component $s_t$,这种成分表达式包含一个预测式和对于每种成分的一个平滑等式,SEM的component form如下。
$$
\begin{aligned}
\text{Forecast equation}: & \quad \hat{y}_{t+h|t} =l_t \\
\text{Smoothing equation}: & \quad l_t =\alpha y_t+(1-\alpha)l_{t-1}
\end{aligned}
$$
由上式可以看出其实在$t+1$时刻的预测值其实就是在$t$时间的$level$。如果我们把上式中的$l_t$和$l_{t-1}$都替换成$y_{t+1|t}$和$y_{t|t-1}$,就可以回复SEM的weighted average form。
1.3. Optimization
上述模型中有平滑参数以及序列模型初始值需要选,但是认为选效果可能不好,这时候就和线性回归一样,可以用如下优化的方式求解,不过模型不是线性模型,所以无法给出解析解,要用软件包来求解。
$$
\text{SSE}=\sum_{t=1}^T(y_t-\hat{y}_{t|t-1})^2
$$
2. Trend Methods
2.1. Holt’s linear trend method
前面提到了SEM模型的component形式里面只包含了level,而包含趋势的表达式则可以写成如下形式。
$$
\begin{aligned}
\text{Forecast equation}: \quad & y_{t+h|t} =l_t+hb_t \\
\text{Smoothing equation}: \quad & l_t =\alpha y_t+(1-\alpha)(l_{t-1}+b_{t-1}) \\
\text{Trend equation}: \quad & b_t = \beta (l_t-l_{t-1})+(1-\beta) b_{t-1}
\end{aligned}
$$
这里$b_t$就是指序列在时间$t$时候的趋势,趋势也是一种斜率其实,所以用$l_t-l_{t-1}$来表示。$0<\beta^*<1$是趋势的平滑参数。
2.2. Damped trend methods
Holt’s linear trend method在预测的时候会产生一个问题,就是在无限地预测未来的时候,会表现出constant trend(increasing or decreasing)。所以就有了这个方法,通过引入一个参数,它可以dampens(抑制)这种constant trend。包含有这种dampen trend的方法已经被证实特别成功,几乎毋庸置疑的它是时间序列预测算法中最流行的一个。除了参数$\alpha$和$\beta^*$,这个方法还引入了一个参数叫做damping parameter $0<\phi<1$。
$$
\begin{aligned}
y_{t+h|t} & = l_t+(\phi+\phi^2+\ldots+\phi^h)b_t \\
l_t & = \alpha y_t+(1-\alpha)(l_{t-1}+\phi b_{t-1}) \\
b_t & = \beta(l_t-l_{t-1})+(1-\beta)\phi b_{t-1}
\end{aligned}
$$
如果$\phi=1$,那这个方法就退化成了与Holt’s linear trend method一样。而对于$0<\phi<1$,它可以抑制这种constant trend。事实上,对于任意的$0<\phi<1$,当$h\to\infty$时,预测都是收敛到$l_T+\frac{\phi}{1-\phi}b_T$,也就是short-run forecast are trended while long-run forecasts are constant。实际应用在,一般设置$0.8<\phi<0.98$。。如下图是当$\phi=0.9$时,某个时间序列的两种方法的趋势预测图。
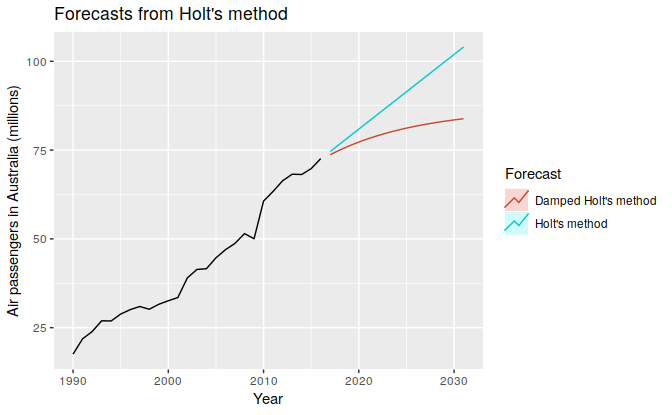
3. Holt-Winters’ Seasonal Method
这个方法可以捕获seasonality,它包含一个forecast equation和三个分别针对level $l_t$,trend $b_t$和seasonal component $s_t$的smoothing equations,它们的smoothing parameters分别是$\alpha, \beta^*,\gamma$。我们使用$m$表示周期性的frequency。例如,一年有四个季度,那么$m=4$,一年有12个月,那么$m=12$。由于周期成分的属性不同,这个方法有两种变体,一种是additive method,一种是multiplicative method。
3.1. Holt-Winters’ additive method
The additive method is preferered when the seasonal variations are roughly constant through the series。它的表达式如下:
$$
\begin{aligned}
\hat{y}_{t+h|t} &=l_t+hb_t+s_{t+h-m(k+1)} \\
l_t & =\alpha (y_t-s_{t-m})+(1-\alpha)(l_{t-1}+b_{t-1}) \\
b_t & =\beta (l_t-l_{t-1})+(1-\beta)b_{t-1} \\
s_t & = \gamma(y_t-l_{t-1}-b_{t-1})+(1-\gamma)s_{t-m}
\end{aligned}
$$
这里$k$是$(h-1)/m$的整数部分,这是为了保证用于预测的周期索引对应最后一年的样本,比如现在按季度为周期,则$m=4$,如果预测10个月以后的数据,则$k=2$,就是以第二年的数据为标准来预测,而非第一年。对于$l_t$,它是对具有周期性质的调整后观测值$y_t-s_{t-m}$和非周期性预测$l_{t-1}+b_{t-1}$之间的平滑。$b_t$采用的就是Holt’s linear method。而$s_t$是当前季节索引$(y_t-l_{t-1}-b_{t-1})$和去年相同周期的季节索引$s_{t-m}$之间的平滑。
季节等式常表达成如下形式:
$$
s_t=\gamma(y_t-l_t)+(1-\gamma)s_{s-m}
$$
如果把平滑函数$l_t$带入进去,可以得到:
$$
s_t=\gamma(1-\alpha)(y_t-l_{t-1}-b_{t-1})+[1-\gamma(1-\alpha)]s_{t-m}
$$
这个和上面的$s_t$平滑等式是一样的。只不过令$\gamma=\gamma^(1-\alpha)$,注意上述四个等式中的$r$都应该是$r^$,则如果令$0<\gamma^*<1$,则$0<\gamma<1-\alpha$
3.2. Holt-Winters’ multiplicative method
The multiplicative method is preferred when the seasonal variations are changing proportional to the level of the series。其表达式如下:
$$
\begin{aligned}
\hat{y}_{t+h|t} & =(l_t+hb_t)s_{t+h-m(k+1)} \\
l_t&=\alpha \frac{y_t}{s_{t-m}}+(1-\alpha)(l_{t-1}+b_{t-1}) \\
b_t &= \beta(l_t-l_{t-1})+(1-\beta)b_{t-1} \\
s_t &= \gamma \frac{y_t}{(l_t+b_{t-1})}+(1-\gamma)s_{t-m}
\end{aligned}
$$
3.3. Holt-Winters’ damped method
和2.2节类似,对$b_t$添加一个参数$\phi$
4. A taxonomy of exponential smoothing methods
其实指数平滑模型还不限于上面提到的内容,通过组合不同的trend和seasonal成分,可以组成9种模型变体。如果用(T,S)表示这个模型包含有trend和seasonal成分,用(A,M)表示这个模型是additive trend和multiplicative seasonality,$(A_d,N)$表示这个模型的damped trend和no seasonality,则9中组合方式见下表。
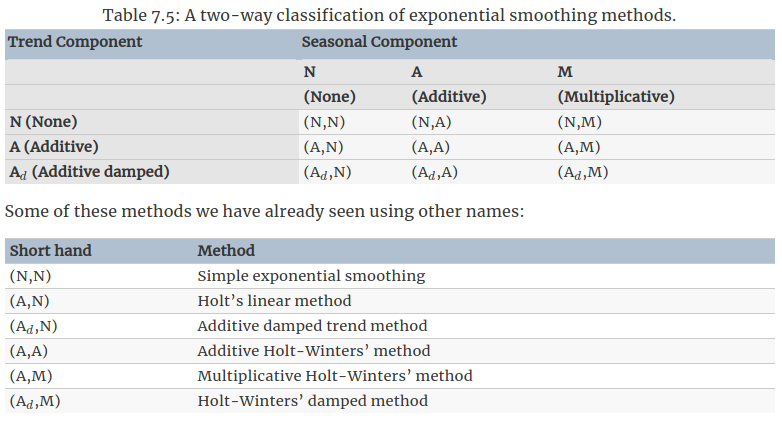
上述组合方式的公式表达如下:
